- The Algebra of Symbols

The Algebra of Symbols (AoS) is a common name for a particular algebraic structure, consisting of the set of symbols and a family of five operations defined on this set. It has been constructed as part of the Kaleidoscope project, and is designed for mathematical modeling of the behavior of Qualitative Dynamical Systems (QDS). The algebra, thus, is a source of symbols used for denoting the values of the variables of the models of the QDSs, representing states of properties of the modeled systems, on the one hand, and of the operations needed for computation of the multivalued qualitative dependence relations of the states of certain variables on the states of some other variables, that determine evolution of the state of the models over time, on the other hand.

Within the project, the AoS is used for creating experimental mathematical models of the QDSs of varying degrees of complexity. So, the meaning of the operations of this algebra is determined by the nature of the qualitative dynamical systems for modeling behavior, of which the AoS is created.

Definition of the Algebra of Symbols

The mathematical structure of the AoS includes:

Domain set of symbols: D = { A, B, C, ..., Z, ... }, whose elements are used for representing states of the modeled qualitative system properties.
Auxiliary set of symbols: X = { -, #, $, ! }, elements of which are intended for representing intermediate values that can be produced in the process of computation of algebraic expressions.
Carrier set of the algebra: S = D U X, defined as a union of the domain set D and auxiliary set X.
Family of five binary operations O = { ?, &, *, |, < }, named: Equivalence, Conjunction, Production, Disjunction, and Application, respectively, defined on the set S.

Definition and Explanation of the Operations

Provided below are definitions of the operations of the Algebra, for visualization and convenience of description of the rules of their work, are presented in the form of small 9 x 9 square tables, framed by the headings of the rows and the columns located on the left and the top sides of the tables, respectively. These headings specify symbols that can be used as the operands of the operations. The symbol located in the upper left corner of the table is the operation symbol. Table cells display output symbols of operations corresponding to the operands listed in the headers of their rows and columns. The tables defining the Equivalence, the Conjunction, the Production, and the Disjunction operations are symmetrical about their main diagonal; that is, of the line connecting their upper left and lower right corners. The order of values passed to these operations as their operands is, therefore, irrelevant. Unlike these four operations, the table defining the Application operation is not symmetrical. Such a definition of this operation is justified by its role in the process of computation of the algebraic expressions, which is described below.

Headers of the tables highlighted with a greenish color indicate the values of the operands used when the operations are applied to compute the qualitative functional dependencies of certain variables in qualitative mathematical expressions on the values of other variables. On the other hand, groups of cells highlighted in the orange color indicate the output of the operations being yielded when they are used for computing these mathematical expressions.

The Equivalence operation

The Equivalence operation is denoted by the symbol "?". It is used in the process of recognition of situations by comparing the current values of a group of variables of a model with the group of constants specifying the expected situation.

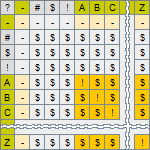
This operation takes two operands, both of which can only be symbols belonging to the set D. It returns the symbol "!", belonging to the set X, when both symbols representing values of the operands turns out to be the same, or the symbol "$", which also belongs to the set X, when both symbols representing values of the operands are different.

The Conjunction operation

The Conjunction operation is denoted by the symbol "&". Similar to the Equivalence operation, this operation is used in the process of recognizing situations. It is applied to the results of the Equivalence operation to confirm that all the results of the comparison of the current state of the variables of the model and their expected values match, and, thus, that the situation is considered as recognized.

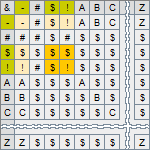
This operation takes two operands, both of which are symbols of the set X. Following the purpose of the operation, its operands can be either the symbol "!" or the symbol "$". Acting like the Boolean conjunction, this operation returns the "!" symbol only in case when both of its operands hold the symbol "!". However, it returns the symbol "$" for all other combinations of values of the operands.

The Production operation

The Production operation is denoted by the symbol "*". Its role in the process of computation of a state equation of the system is to produce the proposed value of the variable of the model, corresponding to the recognized situation. Therefore, it is applied to the result of the recognition of a situation obtained after the utilization of the Equivalence and the Conjunction operations is completed.

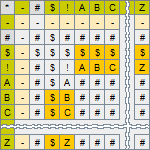
This operation takes two operands, one of which (let's say it is the first one) is the symbol of the set D, and the second is either the symbol "!" or "$", belonging to the set X, and denoting whether the situation is recognized or not recognized. The operation returns the value of the first operand when its second operand states that the situation was recognized, or the symbol "$", i.e., the value of the second operand, when the situation was not recognized.

The Disjunction operation

The Disjunction operation is denoted by the symbol "|". Like the Conjunction operation, it is used after the preceding element-by-element execution of the Production operation. Following its role in the computation of the AoS expressions, its task is to combine all the results of the Production operation.

Each variable of the model can, in the process of modeling the behavior of the system, take different states, denoted by symbols of the set D, corresponding to different situations. Meanwhile, the situations occurring simultaneously may suggest changes of the state of a variable, into either the same or different values. Therefore, the task of the Disjunction operation, in the process of computing the next state of the variables of a model, is to process all the results proposed by the Production operation and to find the only final proposed value that should become the next state of the variable of a model.

This operation takes two operands, each of which can be either a symbol of the set D or a symbol of the set X, and produces a result that may also be either a symbol of the set D or a symbol of the set X. It returns the symbol "$", when none of the expected situations is recognized; a symbol of either operand, when both operands hold the same symbol of the set D, produced as response to different situations; or the symbol "#" when, either the operands hold different symbols of the set D, or when, any one of the operands holds the symbol "#", yielded by this operation during its previous execution.

The Application operation

The Application operation is denoted by the symbol "<", and is the last one in the process of computation of the next value of the variable. Its task is to refine the final proposed value computed by the Disjunction operation, in case when it is not represented by a symbol of the set D, but is one of the symbols: "$" or "#" of the set X. The task, therefore, is to test if the final proposed value belongs to the set D (that is defined) and return it as it is; or, otherwise, when it is a symbol of the set X (that is undefined), to return instead of the undefined value the current value of the variable. That will leave the value of the variable being computed effectively unchanged.

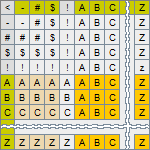
Unlike all other AoS operations, the order of the operands passed to the Application operation is important, and that requires this operation to be non-commutative. Its one operand is the final proposed value of the variable being evaluated, while the other is the current value of this variable. Accordingly, the table defining the operation is organized in such a way that makes the operation to return the final proposed value, when the symbol representing it belongs to the set D, or the current value of the variable, when the final proposed value is undefined, i.e., is represented by any of the symbols belonging to the set X.

All the described operations of the algebra are closed under the set S, and, therefore, can be used in the mathematical expressions written as a composition of the operations. Also, as it can be seen from the definitions of the operations, the auxiliary symbol “-” is the kind of "zero" of the "multiplication" and the "addition" operations of the algebra, and, thus, is the absorption element of both: the Equivalence and the Production operations, while the identity element of both: the Conjunction and the Disjunction operations.

Associativity, Commutativity, and Distributivity Properties of the Operations of the Algebra

Results of testing the operations for their ability to satisfy the laws of associativity, commutativity, and distributivity are presented in Table 1.

Table 1. Result of associativity, commutativity, and distributivity tests conducted for all operations.

This table contains five columns representing the results of testing all five operations: Equivalence, Conjunction, Production, Disjunction, and Application. The result of testing each operation is provided in the form of a row of seven space-separated elements located below the line of separation symbols "~".

The first two elements of the row represent testing results of whether the operation is associative and commutative, while the remaining five elements represent test results of whether the operation is distributive with each of the five operations. These operations are denoted by the first letter of their names, which are located just below the full name of each of the five operations. The adherence of the operations to the associativity law is denoted by the letter A, to the commutativity law by the letter C, and to the distributivity law by the letter D. The case when the result of the test is not confirmed is denoted by the letter N. So, while interpreting the letters: A, C, D, and N, one would say that: